最近细读了 Netflix 关于 A/B 测试的分享, 系列文章链接:
最近自己在实践中开始有一些问题或者一些困扰,但是这一些列文章很好的给出了我们一些解释;
什么是 A/B 测试
来自 WIKI的定义:
A/B测试为一种随机测试,将两个不同的东西(即A和B)进行假设比较[1][2]。该测试运用统计学上的假设检定和双母体假设检定。 A/B测试可以用来测试某一个变量两个不同版本的差异,一般是让A和B只有该变量不同,再测试其他人对于A和B的反应差异,再判断A和B的方式何者较佳
Netflix 举了一个简单的例子:

比如我们想了解将电视用户界面中所有方框图翻转的体验是否对我们的会员有好处。
为了运行实验,我们选取成员的子集(通常是简单的随机样本),然后使用随机分配将该样本均匀地分成两组。“A 组”通常被称为“对照组”,继续获得基本的 Netflix UI 体验,而“B 组”通常被称为“治疗组”,根据有关改善会员的特定假设获得不同的体验经验(更多关于下面的假设)。在这里,B 组收到颠倒的包装盒艺术。
我们等待,然后比较 A 组和 B 组的各种指标的值。一些指标将特定于给定的假设。对于 UI 实验,我们将研究新功能的不同变化组的参与度(engagement)。对于我们不同新的 Feature 变化,可能影响的指标也不一样,比如有的是点击率,有的是播放时长等。
我们需要更为通用的指标
相信大家对 A/B 测试有个最为初步的认知,然而自己在工作中发现,单项的指标并不能完全的去评估本次实验的影响;因为比如比较夸张的 UI 可能吸引更好的点击量,但是并不能成功带领用户观察更多的内容和时长;因此我们需要一些更为通用的指标去佐证。 Netflix则是定义这些为我们的会员带来的快乐和满意度。这些指标包括会员与 Netflix 的互动程度;
除了测试的主要决策指标外,我们还考虑了许多次要指标以及它们将如何受到我们正在测试的产品功能的影响。这里的目标是阐明因果链,从用户行为如何响应新产品体验的变化到我们主要决策指标的变化。
阐明产品变更与主要决策指标变化之间的因果链,并监控该链上的次要指标,有助于我们建立信心,即主要指标中的任何变动都是我们假设的因果链的结果,而不是结果新功能的一些意外后果(或误报 - 在后面的帖子中将详细介绍!
来自用户的投票比领导专家拍板更有说服力
Netflix 分享了过去十年的发展演变,每一次重要的 UI 界面变化都需要有决策参与,做出决定很容易——难的是做出正确的决定。 做出决策的方式有很多:
- 让领导做出所有决定。
- 聘请一些设计、产品管理、用户体验、流媒体交付和其他学科的专家,然+ 后采用他们最好的想法。
- 进行内部辩论,让我们最有魅力的同事的观点占主导地位。
- 复制竞争
在每一种范式中,只有有限数量的观点和视角对决策做出贡献;A/B 测试以及准实验等其他因果推理方法是 Netflix 使用科学方法为决策提供信息的方式。这也是我们通常听到的 Data Driven 最为常见一种;我们形成假设,收集经验数据(包括实验数据),为支持或反对我们的假设提供证据,然后得出结论并产生新的假设;
误报和统计显著性
这个是很重要的概念,让我们去理解A/B 测试结果具有说服力的来源;
假设我们想知道一枚硬币是否不公平,即正面朝上的概率不是 0.5(或 50%)。为了确定硬币是否不公平,让我们进行以下实验:抛硬币 100 次并计算正面结果的比例。由于随机性或“噪声”,即使硬币完全公平,我们也不会期望恰好有 50 个正面和 50 个反面——但是与 50 的偏差有多大才算是“太多”呢?我们什么时候有足够的证据来拒绝硬币实际上是公平的基准断言?如果 100 次抛掷中有 60 次正面朝上,您是否愿意得出硬币不公平的结论?70?我们需要一种方法来调整决策框架并了解相关的误报率。
为了建立直觉,让我们进行一个思考练习。首先,我们假设硬币是公平的——这是我们的“零假设”,它始终是对现状或平等的陈述。然后,我们从数据中寻找反对这个零假设的令人信服的证据。为了决定什么构成令人信服的证据,我们假定空的假设为真,计算每种可能结果的概率。对于抛硬币的例子,假设硬币是公平的,则 100 次抛掷产生 0 次正面、1 次正面、2 次正面,以此类推,直至 100 次正面的概率。跳过数学计算,每个可能的结果及其相关概率都用下图中的黑色和蓝色条显示(暂时忽略颜色)。
然后,我们可以将在硬币公平的假设下计算出的结果概率分布与我们收集的数据进行比较。假设我们观察到 100 次翻转中有 55% 是正面(下图中的红实线)。为了量化这一观察结果是否是硬币不公平的令人信服的证据,我们计算了与我们观察结果不太可能的每个结果相关的概率。在这里,因为我们没有假设正面或反面的可能性更大,所以我们总结了 55% 或更多的翻转正面朝上的概率(红实线右侧的条形)以及 55% 的概率或更多的翻转出现反面(红色虚线左侧的条形)。
这就是神秘的 p 值:如果空假设为真,则看到与我们的观察结果一样极端的结果的概率。在我们的例子中,零假设是硬币是公平的,观察结果是 100 次翻转中有 55% 是正面,p 值约为 0.32。解释如下:如果我们多次重复抛硬币 100 次并用一枚公平的硬币计算正面的比例的实验(原假设为真),那么在 32% 的实验中,结果将是至少 55% 为正面或至少 55% 为反面(结果至少与我们实际观察到的结果一样不可能)。
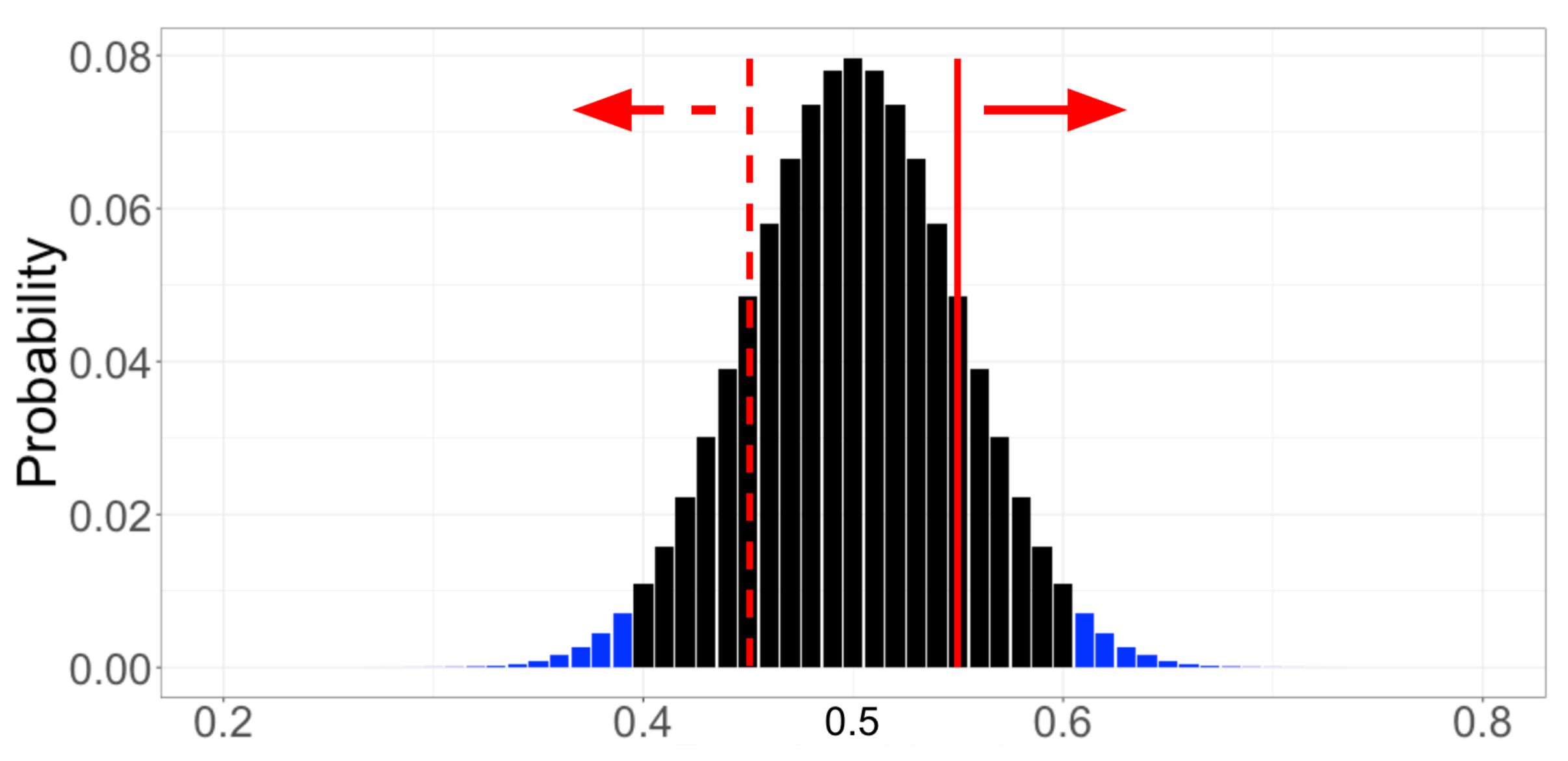
如图抛一枚均匀的硬币 100 次,每次结果的概率表示为正面的比例。
我们如何使用 p 值来确定是否有统计上显着的证据表明代币不公平,或者我们的新产品体验是对现状的改进?回到我们一开始同意接受的 5% 误差率:我们得出结论,如果 p 值小于 0.05,则存在统计上显着的影响。这形式化了这样的直觉:如果我们的结果在公平硬币的假设下不太可能发生,那么我们应该拒绝硬币是公平的原假设。在观察 100 次抛硬币中 55 次正面朝上的示例中,我们计算出 p 值为 0.32。由于 p 值大于 0.05 显着性水平,因此我们得出结论,没有统计上显着的证据表明硬币是不公平的。
我们可以从实验或 A/B 测试中得出两个结论:我们要么得出结论有效果(“硬币不公平”,“前 10 个功能提高了会员满意度”),要么得出结论没有足够的证据得出有影响的结论(“不能得出硬币不公平的结论”,“不能得出前 10 行增加会员满意度的结论”)。这很像陪审团审判,两种可能的结果是“有罪”或“无罪”——而“无罪”与“无罪”有很大不同。同样,这个(常客)A/B 测试方法不允许我们得出没有影响的结论——我们永远不会得出硬币是公平的,或者新产品功能对我们的会员没有影响的结论。我们只是得出结论,我们没有收集到足够的证据来拒绝没有差异的零假设。在上面的硬币示例中,我们在 100 次抛掷中观察到 55% 的正面朝上,并得出结论,我们没有足够的证据将硬币标记为不公平。重要的是,我们并没有得出这枚硬币是公平的结论——毕竟,如果我们收集更多的证据,比如将同一枚硬币抛掷 1000 次,我们可能会找到足够令人信服的证据来拒绝公平性的原假设。
如何建立对决策信心
A/B 测试的一个令人不快的现实是,没有任何测试结果能够反映根本事实。正如我们在之前的文章中所讨论的,良好的做法包括首先设置和了解误报率,然后设计一个功能强大的实验,以便有可能检测到合理且有意义的真实效果。这些来自统计学的概念帮助我们减少和理解错误率,并在面对不确定性时做出正确的决策。但目前还没有办法知道特定实验的结果是假阳性还是假阴性。这些考虑因素与美国统计协会 2016 年关于统计显着性和 P 值的声明一致,其中以下三个直接引用(粗体)都为我们的实验实践提供了信息:
- 正确的推断需要完整的报告和透明度
- p 值或统计显着性并不能衡量效果的大小或结果的重要性
- 科学结论以及商业或政策决策不应仅基于 p 值是否超过特定阈值
总的来说这一系列非常经典,大家看恶意细读;无论你是从事数据科学还是研发人员,都值得去学习这背后的原理和方法论;
